Peut-on ralentir la propagation du SARS-CoV-2 en protégeant les super-contaminateurs ?
Plusieurs études ont montré que la circulation du SARS-CoV-2 est étroitement liée au phénomène de la super-propagation : quelques individus infectés en forte interaction sociale sont responsables d’un très grand nombre de contaminations, là où une majorité n’infecte qu’une ou deux personnes au plus. Ce fait est sous-évalué par les modèles de diffusion de l’épidémie utilisés pour l’aide à la décision publique. Les rares modèles qui prennent en compte ce phénomène, cantonnés pour l’heure au monde académique, le font en reliant la super-propagation au contexte dans lequel certains épisodes de super-propagation ont été observés, notamment lors de rassemblements de taille variée dans des espaces confinés. Dans un article paru dans le Journal of Artificial Societies and Social Simulation, des chercheurs du CNRS et de l'European University Institute (Italie) proposent une approche différente, en s’appuyant sur la théorie des réseaux sociaux pour penser le phénomène de la super-propagation.
Gianluca Manzo, chargé de recherche CNRS au sein du Groupe d'étude des méthodes de l'analyse sociologique de la Sorbonne (GEMASS, UMR8598, CNRS / Sorbonne Université), et Arnout van de Rijt, professeur de sociologie à l’European University Institute, ont intégré la configuration des interactions sociales dans les modèles épidémiologiques, en privilégiant le nombre et l’agencement des contacts sociaux entre individus plutôt que leurs caractéristiques physiologiques. Ils mettent ainsi en évidence le fait que le super-propagateur est un individu qui, pour des raisons structurelles (son occupation, par exemple) et/ou par son style de vie, entretient des contacts sociaux journaliers plus élevés et variés que la moyenne. Il présente ainsi un risque accru d’être contaminé et de contaminer à son tour un nombre d’individus élevé. Bien que statistiquement rares, ces acteurs aux interactions nombreuses et éparpillées seraient donc responsables de la plupart du trafic viral ainsi que de la vitesse de propagation du virus. C’est pourquoi les chercheurs ont souhaité s’intéresser prioritairement aux personnes ayant de nombreuses interactions sociales afin de développer un modèle informatique permettant de contenir la diffusion du virus.
Leur étude procède en trois temps. En exploitant les résultats d’une enquête effectuée sur un échantillon représentatif de 2 000 personnes durant laquelle celles-ci devaient noter toutes leurs rencontres physiques durant deux jours, les chercheurs montrent que les contacts journaliers des français sont mal décrits par le nombre de contacts moyen : des individus ayant un nombre de contacts beaucoup plus élevé que la moyenne sont bien présents dans la population (Figure 1). Puis, ils construisent une simulation informatique dans laquelle chaque individu est représenté par un agent artificiel ; le réseau de rencontres reliant ces agents reproduit l’hétérogénéité des contacts sociaux observée dans la population française. Au sein de ce monde virtuel, ils simulent enfin la circulation du virus et évaluent l’efficacité relative d’intervenir de façon prioritaire sur un nombre limité de super-propagateurs (les individus ayant un très grand nombre de contacts sociaux) plutôt que de façon uniforme sur l’ensemble de la population.
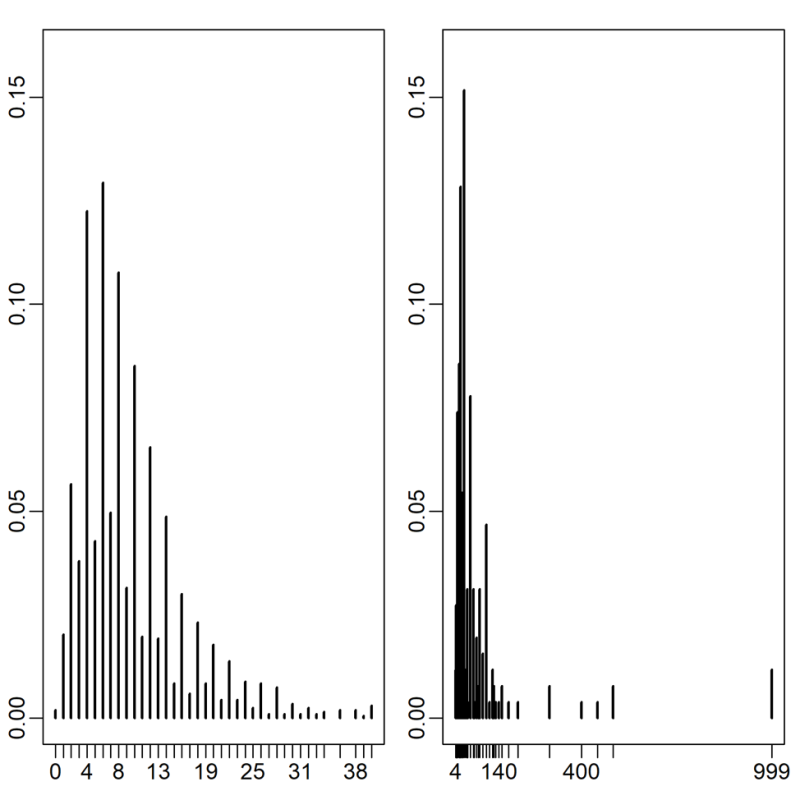
Figure 1. Gauche: Proportion de répondants (ordonnée) déclarant un nombre x de contacts rapprochés journaliers (moyenne des deux jours d’observation) (abscisse) (n=2,033); Droite: Proportion de répondants (ordonnée) déclarant un nombre x de contacts rapprochés journaliers strictement liés au travail (abscisse) parmi les répondants qui considèrent leur métier comme étant particulièrement exposé aux contacts sociaux (n=257).
Les chercheurs simulent deux stratégies d’identification des super-propagateurs :
- Selon la première stratégie, les agents virtuels représentant les individus réels sont rangés selon l’ordre du nombre de leurs contacts sociaux (du plus grand au plus petit) si bien que ceux ayant davantage d’interactions sont testés/vaccinés en premier.
- Selon la seconde stratégie, une fraction d’agents virtuels est sélectionnée au hasard et, pour chaque agent sélectionné, un seul de ses contacts, également choisi au hasard, est testé/vacciné.
Cette dernière méthode exploite une propriété profonde des réseaux d’interactions sociales, connue sous le nom de « paradoxe de l’amitié » : elle permet d’identifier les individus ayant un nombre d’interactions sociales plus élevé que l’individu moyen sans exiger que l’on connaisse le nombre exact de contacts sociaux de chaque individu dans la population.
Les simulations montrent qu’intervenir directement sur les super-propagateurs est toujours plus efficace qu’intervenir de manière uniforme sur la population. Selon la condition expérimentale retenue, le pic épidémique pourrait être réduit de 10 à environ 97 % (Figure 2).
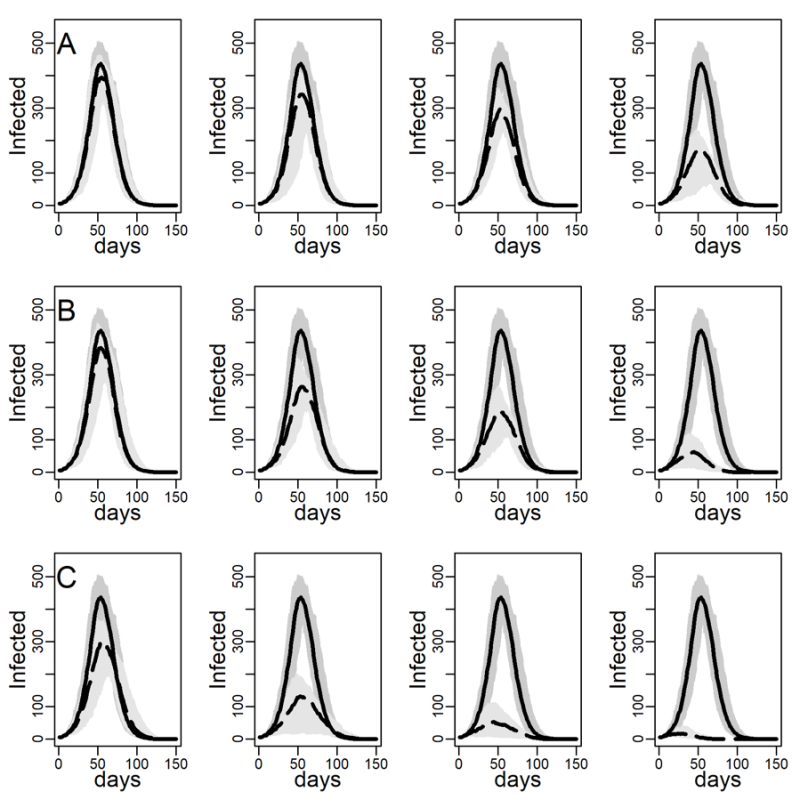
Figure 2. Nombre d’agents infectés (ordonnée) par jour (abscisse) (médiane de 100 réplications) sous les trois interventions (lignes) ciblant 1, 3, 5, ou 10 agents par jours (colonnes). A – Intervention sans cible (les agents à immuniser sont sélectionné au hasard); B – Intervention sur les super-propagateurs identifiés par la méthode du cas-contact (l’agent à immuniser est choisi au hasard parmi les contacts d’un agent donné, choisi lui aussi au hasard). C – Intervention sur les super-propagateurs identifié par la méthode du dégrée décroissant (les agents à immuniser sont sélectionné en fonction du nombre de leurs contacts sociaux, progressivement du plus haut au plus petit). La limite supérieure et inférieure des aires grisées correspondent aux 5ème et 95ème percentiles de 100 réplications. Ligne continue: Simulations sans interventions; Ligne en pointillé: Simulation avec l’intervention. Probabilité de transmission dyadique r=0.05 & Niveau de recoupement des contacts sociaux (Cc=0.01). n = 2,029 agents.
Référence
Manzo G., van de Rijt A. 2020, Halting SARS-CoV-2 by Targeting High-Contact Individuals, Journal of Artificial Societies and Social Simulation 23(4) 10.